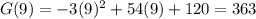For this question the store earnings are:
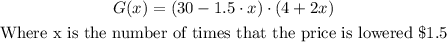
Now, we use the first and second derivative criteria to maximize G(x).
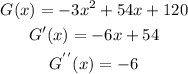
Setting G'(x)=0 and solving for x we get:

Since G''(9)=-6<0, the function has a maximum when x=9. Finally, the maximum income for the school store is: