Question

How do I figure out the mean and how do I get the median of the number x from the following data?

Answer 1

Given the table

The values in the first row (x) indicate the possible values of the variable.

The values in the second row (f) indicate the frequency, which is the number of times that a determined value was observed.

Mean

To calculate the mean value of the data set, you have to multiply each value of the variable by its observed frequency, add the results and divide it by the sample size, following the formula:

`\bar{x}=(\Sigma x_if_i)/(n)`

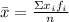
To determine the sample size, you have to sum the observed frequencies:

`\begin{gathered} n=3+8+17+32+22+8 \\ n=90 \end{gathered}`

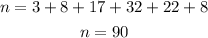
Calculate the mean:

`\begin{gathered} \bar{x}=((99.6*3)+(99.7*8)+(99.8*17)+(99.9*32)+(100*22)+(100.1*8))/(90) \\ \bar{x}=(8989.7)/(90) \\ \bar{x}=99.89\cong99.9 \end{gathered}`

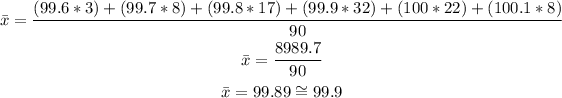
Median

To calculate the median, you have to determine its position first. To find the position of the median, you have to use the following formula:

`\begin{gathered} PosMe=((n+1))/(2) \\ PosMe=(90+1)/(2) \\ PosMe=(91)/(2) \\ PosMe=45.5 \end{gathered}`

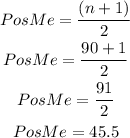
The position of the median is 45.5, to determine the value, the first step is to calculate the accumulated frequencies for each category.

The position of the median is 45.5, which means that you can find its value between positions 45 and 46.

If you look at the accumulated frequencies, both of these observations are found in the fourth category of the variable, their value is 99.9.

To determine the value of the median, you have to average both observations:

`\begin{gathered} Me=(45th+46th)/(2) \\ Me=(99.9+99.9)/(2) \\ Me=(199.8)/(2) \\ Me=99.9 \end{gathered}`

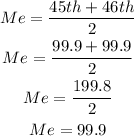
The median of the data set is 99.9.