First, calculate the mean of the scores. Since there are 10 scores, then the mean is given by:
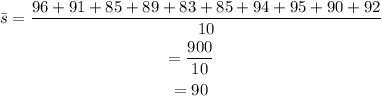
Calculate the absolute value of the difference between the mean and each of the scores:
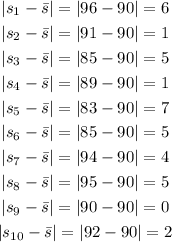
The mean absolute deviation is the average of the absolute deviations from each score to the mean. Calculate the mean from the deviations:
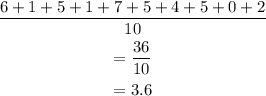
Therefore, the mean absolute deviation of Taylor's scores, is 3.6