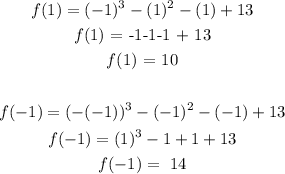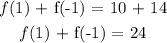f(0) = 13
f(2) = -1
f(-2) = 19
f(1) + f(-1) = 24
Step-by-step explanation:
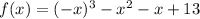
for f(0): we will substitute x with 0 in the function
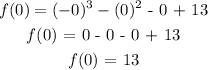
for f(2): we wil substitute x with 2 in the function
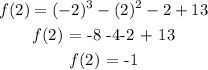
for f(-2): we will substitute x with -2 in the function
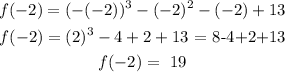
for f(1) + f(-1): we will find f(1) and f(-1) seperately, then we will sum the result