Question

Suppose that a researcher is interested in estimating the mean systolic blood pressure, μ, of executives of major corporations. He plans to use the blood pressures of a random sample of executives of major corporations to estimate μ. Assuming that the standard deviation of the population of systolic blood pressures of executives of major corporations is 24 mm Hg, what is the minimum sample size needed for the researcher to be 95% confident that his estimate is within 3 mm Hg of μ?Carry your intermediate computations to at least three decimal places. Write your answer as a whole number (and make sure that it is the minimum whole number that satisfies the requirements).

Answer 1

In order to find the sample size, we can use the following formula that relates the population and sample standard deviations:

`\sigma_{\bar{x}}=z(\sigma)/(√(n))`

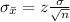
For a confidence interval of 95%, we have z = 1.96.

Then, using the values of the standard deviations, we have:

`\begin{gathered} 3=1.96(24)/(√(n))\\ \\ 3=(47.04)/(√(n))\\ \\ √(n)=11.76\\ \\ n=138.3 \end{gathered}`

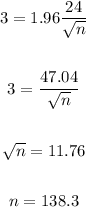
Rounding to the next whole number, we have a sample size of 139.