Given:
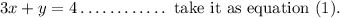
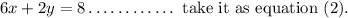
Multiply both sides of the equation (1) by 2, we get
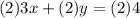
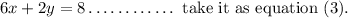
Subtract equation (2) from equation (3), we get
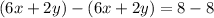

We obtain equation (2) by multiplying 2 and equation (1).
Equation 2 is dependent on equation (1).
We know that a dependent system has an infinite number of solutions.
The solution of the system has many solutions.