Concept
Apply z scores
First, let's find the z-score that corresponds to the information given for Exam A.

For Sophie to do equivalently well in Exam B as well as she did on Exam A, we find the value of x by using the z score of exam A.
The formula for finding a z-score is shown below:
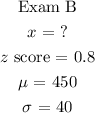
Next, substitute the following values to find the value of x.
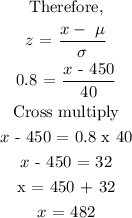
Final answer
x = 482