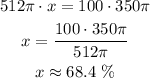Question

What is container B that is full after the pumping is complete ?

Answer 1

68.4%

Explanation

The volume of a cylinder is calculated as follows:

`V=\pi r^2h`

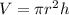
where r is the radius and h is the height of the cylinder.

In the case of cylinder A, its radius is r = 5 ft (= 10/2) and its height is h = 14 ft. Then, its volume is:

`\begin{gathered} V_A=\pi\cdot5^2\cdot14 \\ V_A=350\pi\text{ ft}^3 \end{gathered}`

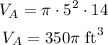
In the case of cylinder B, its radius is r = 8 ft (= 16/2) and its height is h = 8 ft. Then, its volume is:

`\begin{gathered} V_B=\pi\cdot8^2\cdot8 \\ V_B=512\pi\text{ ft}^3 \end{gathered}`

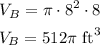
After the pumping is completed all the liquid in cylinder A, which was full, is placed in cylinder B. If the volume of cylinder B represents 100%, then we need to find what percent, x, represents the volume of cylinder A. We can do this with the help of the next proportion:

`\frac{512\pi\text{ ft}^3}{350\pi\text{ ft}^3}=\frac{100\text{ \%}}{x\text{ \%}}`

Solving for x:

`\begin{gathered} 512\pi\cdot x=100\cdot350\pi \\ x=(100\cdot350\pi)/(512\pi) \\ x\approx68.4\text{ \%} \end{gathered}`