Question

the length of the rectangle is 7m more than double the width and the area is 99m to the second power find the dimensions

Answer 1

We know that

• The length is 7 meters more than double the width.

,

• The area is 99 square meters.

First, we express the relationship between the length and the width.

`l=7+2w`

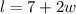
We know that the area is

`A=l\cdot w`

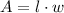
Replacing the first expression, and the area.

`99=(7+2w)\cdot w`

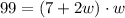
Let's solve for w.

`\begin{gathered} 99=7w+2w^2 \\ 2w^2+7w-99=0 \end{gathered}`

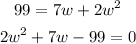
Now, we use the quadratic formula.

`w_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where a = 2, b = 7, and c = -99. Let's replace all these values in the formula.

`\begin{gathered} w_(1,2)=\frac{-7\pm\sqrt[]{7^2-4\cdot2\cdot(-99)}}{2(2)}=\frac{-7\pm\sqrt[]{49+792}}{4} \\ w_(1,2)=\frac{-7\pm\sqrt[]{841}}{4}=(-7\pm29)/(4) \end{gathered}`

Now, we rewrite it into two equations.

`\begin{gathered} w_1=(-7+29)/(4)=(22)/(4)=5.5 \\ w_2=(-7-29)/(4)=-(36)/(4)=-9 \end{gathered}`

The width is 5.5 meters because it can't be represented by a negative number.

We use the width to find the length.

`\begin{gathered} l=7+2w \\ l=7+2(5.5) \\ l=7+11=18 \end{gathered}`

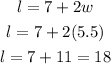
The length is 18 meters.

Therefore, the dimensions are 5.5 meters wide and 18 meters in length.