Question

find the radius of a circle which had a sector of area 15 square feet determined by a central angle 1/2 radian.

Answer 1

The radius of the circle is approximately 7.75 feet.

To find the radius of a circle with a sector of area 15 square feet determined by a central angle of 0.5 radians, we can use the formula for the area of a sector:

`\[ \text{Area of sector} = (1)/(2) r^2 \theta \]`

Where:

-
`\( r \)` is the radius of the circle.

-
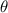`\( \theta \)` is the central angle of the sector in radians.

Given:

- The area of the sector is 15 square feet.

- The central angle
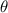`\( \theta \)` is 0.5 radians.

We can rearrange the formula to solve for the radius
`\( r \)`:

`\[ 15 = (1)/(2) r^2 * 0.5 \]`

`\[ 15 = (1)/(4) r^2 \]`

`\[ r^2 = 15 * 4 \]`

`\[ r^2 = 60 \]`

`\[ r = √(60) \]`

Now let's calculate the exact value of
`\( r \).`

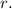
The radius of the circle is approximately 7.75 feet.

Answer 2

radius = 7.746 feet

Step-by-step explanation:
`\begin{gathered} \text{Area of sector with angle in degr}ees\colon \\ Areaofasector=\theta/360*\pi r^(2) \end{gathered}`

the angle is in radian:

`\text{Area of sector = 1/2 }r^2\text{ }\theta`
`\begin{gathered} Areaof\text{ sector = 15 square f}eet \\ \theta\text{ = 1/2 radian} \\ 15\text{ = }(1)/(2)* r^2*(1)/(2) \end{gathered}`
`\begin{gathered} 15\text{ = }(r^2)/(4) \\ 15(4)=r^2 \\ 60=r^2 \end{gathered}`
`\begin{gathered} r\text{ = }\sqrt[]{60} \\ r\text{ = 7}.746\text{ f}eet \end{gathered}`