Question

state the power function that the graph of f resembles for large values of x. then find the end behavior for the function. write your findings using limit notation(show all work)

Answer 1

We are given the following function

`y=(x-1)^3`

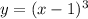
The real zero of the function is x = 1

The multiplicity of the function is 3

The graph of the function looks like below

As you can see, the function falls to the left and rises to the right.

Since the multiplicity of the function is 3, the end behavior of the function will be

`y=x^3`

Using the limit notation, we can write

`\lim _(x\rightarrow\infty)y=x^3`

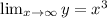
As the value of x grows larger (approaches infinity) the end behavior of the function resembles y = x³