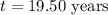Answer:
The time it will take for this investment is;
Step-by-step explanation:
Given that the initial investment was $6,000.
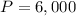
And the final amount is $27,696.
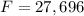
at an annual rate of 8%, compounded semiannually;
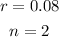
Recall that the formula for calculating compound interest can be written as;
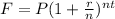
Where t is the time of investment.
Making t the subject of the formula;
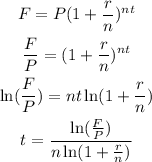
Substituting the given values;
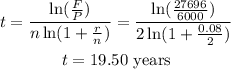
Therefore, the time it will take for this investment is;