Question

Throughout this semester we have learned about scatterplots and lines of best fit, solving systems ofequations, exponents, radicals, operations on polynomials, solving quadratic functions, and graphingquadratic functions. (Pick One) Describe how you can use any (ONE) of those topics in the realworld. Be thorough in your response.

Answer 1

Step-by-step explanation

Systems of equations

Juan´s age is 4 times the Peter's age, and

eigth years from now the Juan's age will be 36

so, we can solving a system of equations to solve this.

Step 1

let x represents the Juan´s age

let y represents the Peter´s age

so.

Juan´s age is 4 times the Peter's age,so

`x=4y\rightarrow equation(1)`

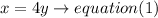
and

eigth years from now the Juan's age will be 36

`\begin{gathered} add\text{ 8 to both ages, } \\ x+8=36\rightarrow equation(2) \\ \end{gathered}`

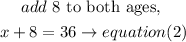
Step 2

solve the equations

a)solve equation (2)

`\begin{gathered} x+8=36 \\ subtract\text{ 36 in both sides} \\ x+8-8=36-8 \\ x=28 \end{gathered}`

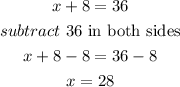
it means Juan's age is 28

b) replace the x value into equation (1)

`\begin{gathered} x=4y\rightarrow equation(1) \\ 28=4y \\ \text{divide both sides by 4} \\ (28)/(4)=(4y)/(4) \\ 7=y \end{gathered}`

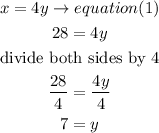
hence, the Peter's agte is 7

I hope this helps you