Answer:
![\sqrt[9]{10}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/rdvklr172r2qjcgl8m1e4m.png)
Explanation:
When you're multiplying radicals you start by multiplying inside the radical. Break it down so it's easier for you:
1.
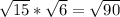 beacause 15 * 6 = 90
beacause 15 * 6 = 90
2. The next step is to simplify that radical. You simplify by finding factors of that number. The factors of 90 are:
- 1 * 90
- 2* 45
- 3 * 30
- 5 * 18
- 6 * 15
- 9 * 10
You want to take the biggest factors of that number (yours is 9 * 10). After that you are going to break it down more. What are the factors of 9 and what are the factors of 10? Well the biggest factors of 9 are 3 * 3 and the biggest factors of 10 are 5 * 2, so 10 cannot be broken down anymore because it doesn't have two of the same numbers so 10 is going to stay the same, but 9 has two of the same number (3). What we're left with is
![\sqrt[3]{10}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/e9kimebf4s25ta94o295kz.png) because the same numbers stay out of the radical and the single number stays inside.
because the same numbers stay out of the radical and the single number stays inside.
3. We can't forget about the 3 that we left out, so what we're going to do is write
![3 *\sqrt[3]{10}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/st4j56iu45l7qepegj06of.png) . When you multiply that out you keep the outside with the outisde which results in the answer being
. When you multiply that out you keep the outside with the outisde which results in the answer being
![\sqrt[9]{10}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/high-school/rdvklr172r2qjcgl8m1e4m.png) because this cannot be simplified anymore.
because this cannot be simplified anymore.