Question

Multiplying radicals. Simplify

Answer 1

`\sqrt[9]{10}`

Explanation:

When you're multiplying radicals you start by multiplying inside the radical. Break it down so it's easier for you:

1.
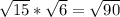`√(15)*√(6) = √(90)` beacause 15 * 6 = 90

2. The next step is to simplify that radical. You simplify by finding factors of that number. The factors of 90 are:

• 1 * 90
• 2* 45
• 3 * 30
• 5 * 18
• 6 * 15
• 9 * 10

You want to take the biggest factors of that number (yours is 9 * 10). After that you are going to break it down more. What are the factors of 9 and what are the factors of 10? Well the biggest factors of 9 are 3 * 3 and the biggest factors of 10 are 5 * 2, so 10 cannot be broken down anymore because it doesn't have two of the same numbers so 10 is going to stay the same, but 9 has two of the same number (3). What we're left with is
`\sqrt[3]{10}` because the same numbers stay out of the radical and the single number stays inside.

3. We can't forget about the 3 that we left out, so what we're going to do is write
`3 *\sqrt[3]{10}`. When you multiply that out you keep the outside with the outisde which results in the answer being
`\sqrt[9]{10}` because this cannot be simplified anymore.