For this problem, we are provided with the following expression:
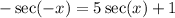
We need to solve it for x over the interval [0, 2pi).
We have:
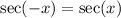
Therefore, we can replace the left side of the equation as shown:
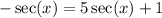
Now we need to isolate the sec(x) on the left side.
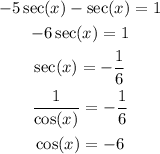
Now we can apply the arc cosine to determine the value of x.
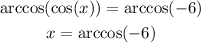
There are no real values for x that have a cosine equal to -6. Therefore, this problem has no real solution.