Given:
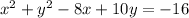
Required:
To find the center and radius of the given circle equation.
Step-by-step explanation:
Consider the given equation,
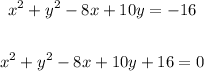
Now add and subtract 25 t the given equation ,
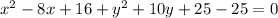
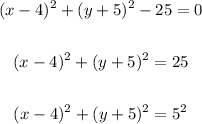
Therefore,
The center is : (4,-5)
The radius is : 5
Final Answer:
The center is : (4,-5)
The radius is : 5