Question

Find two consecutive odd integers such that the sum of their squares is 514.

Answer 1

Given:

The sum of the squares of two consecutive odd integers is 514.

Required:

Find the integers.

Step-by-step explanation:

Let two consecutive odd integers be x, x+2.

According to the question

`\begin{gathered} x^2+(x+2)^2=514 \\ x^2+x^2+4x+4=514 \\ 2x^2+4x-510=0 \\ x^2+2x-255=0 \end{gathered}`

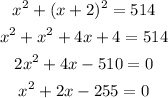
This is the quadratic equation.

Solve it by using the middle-term splitting method.

`\begin{gathered} x^2+17x-15x-255=0 \\ x(x+17)-15(x-17)=0 \\ (x+17)(x-15)=0 \end{gathered}`

`\begin{gathered} x+17=0 \\ x=-17 \end{gathered}`
`\begin{gathered} x-15=0 \\ x=15 \end{gathered}`

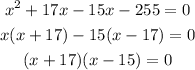
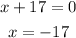
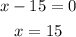
When x=-17 then consecutive odd integer = -17+5 = -15

When x= 15 then consecutive odd integer =15+ 2 = 17

Final Answer:

The consecutive odd integer