Question

Use the information given to find the equation of the line using the point-slope formula (y-y_1)=m(x-x_1)). Then convert your answer to slope-intercept form (y=mx+b).y-intercept of 2 and (4,-1)To earn full credit be sure to clearly identify your point slope equation and your slope intercept equation. Include all steps and calculations.

Answer 1

Given two points that the line goes through,

y intercept of 2, this corresponds to (0, 2)

(4, -1)

We have,

`\begin{gathered} (x_1,y_1)=(0,2) \\ (x_2,y_2)=(4,-1) \end{gathered}`

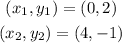
The point slope formula is,

`y-y_1=m(x-x_1)`

Where

m is the slope and,

`m=(y_2-y_1)/(x_2-x_1)`

So, let's substitute the points into the point slope form of the line and re-arrange to slope intercept form. The steps are shown below:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-2=(-1-2)/(4-0)(x-0) \\ y-2=-(3)/(4)(x-0)-------\text{ Point Slope Form} \\ -------------------------------------- \\ \text{Then, we re-arrange to slope intercept form (y = mx + b):} \\ y-2=-(3)/(4)(x) \\ y-2=-(3)/(4)x \\ y=-(3)/(4)x+2----------\text{Slope Intercept Form} \\ -------------------------------------- \end{gathered}`Answer
`\begin{gathered} y-2=-(3)/(4)(x-0)-------\text{ Point Slope Form} \\ y=-(3)/(4)x+2----------\text{Slope Intercept Form} \end{gathered}`