When we have a normal distribution for a randome variable X we know its mean μ and its standard deviation σ.
We can normalize this function to the standard normal distribution (mean 0 and standard deviation 1) by calculating the z-score for any value of X.
This can be done as:
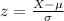
Percentiles can be asociated to its corresponding z-score.
For example, percentil 30th correspond approximately to z = -0.5.
Then, using the previous equation, if we know z we can calculate its corresponding X as:
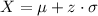
This converts the standard normal distribution back into the distribution that corresponds to X.
Answer: X = μ + zσ [First option]