The given information is:
- The bank loaned out $17,000.
- One part at a rate of 8% and the rest at 16%, per year.
- The total interest received in one year totaled $2000.
Let's set x the part loaned at 8% and y the part loaned at 16%. So:
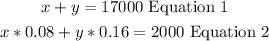
First, find x in terms of y from equation 1:
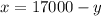
Now, replace x in equation 2 and solve for y:
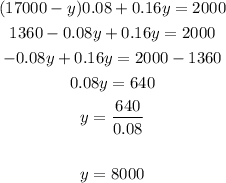
Replace y in and solve for x:
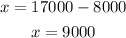
So, the bank loaned $9000 at 8% and $8000 at 16%.