Question

it is presentation day in class and your instructor is drawing names from a hat to determine the order of the presentations. if there are 18 students in the class, what is the probability that the first 2 presentations will be by Kelly and Brooke, in that order? express your answer as a fraction

Answer 1

Given that the order actually matters, we use the permutation formula.

`P(n,r)=(n!)/((n-r)!)`

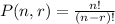
Where n = 18 and r = 2.

`P(18,2)=(18!)/((18-2)!)=(18\cdot17\cdot16!)/(16!)=18\cdot17=306`

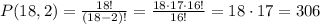
There are 306 ways to arrange the students in groups of two.

Then, we find the probability by dividing 1/306 because there's one possible event of being Kelly and Brooke the first 2 out of 306 possible permutations

Therefore, the probability is 1/306.