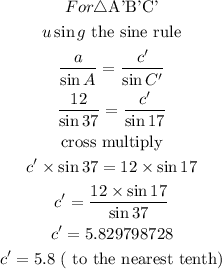Solution
Let the triangle be
First We will find angle B
Note 1: The sine rule
Using the sine rule
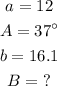
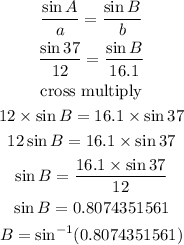
Now, notice that
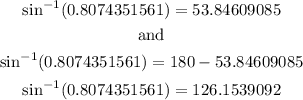
Now we return back to

Since we have two values of B, then this measurement produce two (2) triangles
The two triangles will be
We have already computed angle C and C' for the two triangles
The workings is as shown below
Note 2: Sum of angles in a triangle is 180 degrees
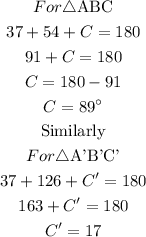
To find the sides c and c'
First Triangle
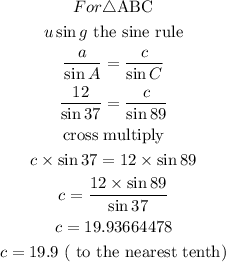
Second Triangle