Question

Select the correct answer.What are the roots of this equation?32 – 40 + 9 = 0O A. 1 15OB. 2 + 15OC. 2 + iv3OD. 1 iv52

Answer 1

Given :

`x^2\text{ - 4x + 9 = 0}`

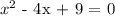
Solution

To find the roots of the equation, we can try factorizing the expression by the left.

The factors of 9 are 3,3 or 1, 9. Each of these cannot work.

So, we use the quadratic formula instead.

Given the general form of a quadratic equation:

`ax^2\text{ + bx + c = 0}`

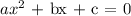
The quadratic formula to find the roots of the equation is given as:

`\text{x = }\frac{-b\text{ }\pm\sqrt[]{b^2-4ac}}{2a}`

Comparing the standard form with the given equation, we have:

a = 1 , b = -4, c =9

Substituting this into the quadratic formula:

`\begin{gathered} x\text{ = }\frac{-(-4)\text{ }\pm\sqrt[]{(-4)^2-\text{ 4}*1*9}}{2\text{ }*\text{ 1}} \\ =\text{ }\frac{4\text{ }\pm\text{ }\sqrt[]{-20}}{2} \\ =\text{ }\frac{4\text{ }\pm\text{ }\sqrt[]{4\text{ }*\text{ -5}}}{2} \\ =\text{ }\frac{4\text{ }\pm\text{ 2}\sqrt[]{-5}}{2} \\ =\text{ }\frac{4\text{ }\pm\text{ 2}\sqrt[]{5}i}{2} \\ \text{recall that i = }\sqrt[]{-1} \\ x\text{ = 2 }\pm\text{ i}\sqrt[]{5} \end{gathered}`

Answer: Option B