Question

Which of the following would be parallel to the graph of 2x -3y = 18?

Answer 1

We need to analyze each case separately:

We also need to remember that for two lines to be parallel they need to have the same slope. We can transform the equation in the slope-intercept form to find these slopes. This is a way to do so.

1. In the first case, we need to find the slope-intercept form of the equation. It is:

`2x+3y=18\Rightarrow3y=18-2x\Rightarrow y=(18)/(3)-(2)/(3)x\Rightarrow y=-(2)/(3)x+6`

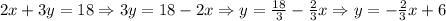
This line is not parallel to the one given, since the slope-intercept form of the given linear equation is:

`2x-3y=18\Rightarrow-3y=18-2x\Rightarrow y=(18)/(-3)+(-2)/(-3)x\Rightarrow y=(2)/(3)x-6`

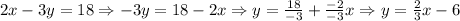
Then, the slope is m = 2/3, and the slope, in this case, is m = -2/3. Therefore, in this first case, the lines are not parallel. Not parallel.

2. The second equation is y = 2/3x +1, then, this line is parallel to the given in the question. It is parallel (m = 2/3).

3. We need to transform the third equation in the slope-intercept form:

`-2x-3y=-18\Rightarrow-3y=-18+2x\Rightarrow y=-(2)/(3)x+6`

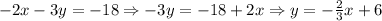
The slope, in this case, is the inverse of the slope given in the question. It is not parallel to the given equation. Not parallel.

4. In the last case, we have that the slope is, for the second equation, also m = -2/3. Then, this line is not parallel to the one given in the question. Not parallel.