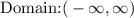Question

Looking to find the requested function and state the domain.Find g o f for f(x)=10x-5 and g(x)=3x+6

Answer 1

`(g\circ f)(x)=30x-9,\text{Domain:(}-\infty,\infty)`

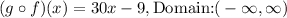
Step-by-step explanation:

Given the functions f(x) and g(x) defined as follows:

`\begin{gathered} f\mleft(x\mright)=10x-5 \\ g\mleft(x\mright)=3x+6 \end{gathered}`

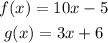
The composite function g o f is defined below:

`\begin{gathered} (g\circ f)(x)=g(f(x)) \\ =3f(x)+6 \\ =3(10x-5)+6 \\ =30x-15+6 \\ (g\circ f)(x)=30x-9 \end{gathered}`

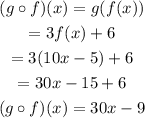
The domain of the function is the set of all possible values of x.

In the composite function, x can take on any value in the real line. Therefore:

`\text{Domain:(}-\infty,\infty)`