Question

Solve the inequality and graph your solution. -4x+2<-6

Answer 1

We are given the following inequality

`-4x+2<-6​`

Let us solve this inequality

Step 1:

Subtract 2 from both sides of the inequality

`\begin{gathered} -4x+2-2<-6​-2 \\ -4x<-8 \end{gathered}`

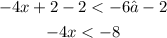
Step 2:

Divide both sides of the inequality by -4

Note that whenever you multiply or divide by a negative number then the direction of the inequality changes.

`\begin{gathered} -(4x)/(-4)<-(8)/(-4) \\ x>2 \end{gathered}`

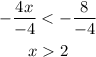
So the solution is x > 2 (all values greater than 2)

Now let us graph this solution

As you can see, all the values greater than x > 2 is the solution