Answer:
a) Graphing the function we have;
Therefore, the amount he saves after 5 weeks is $120
b) The relationship is not proportional because the corresponding values are not proportional and do not pass through the origin.
Step-by-step explanation:
Given the data in the table.
We can extrapolate to derive the Amount saved in the following weeks;
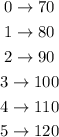
Graphing the function we have;
Therefore, the amount he saves after 5 weeks is $120
To determine if the relationship is proportional or not.
For it to the proportional;
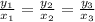
substituting the values from the table or graph, we have;
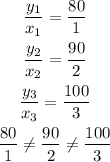
Therefore, the relationship is not proportional because the corresponding values are not proportional and do not pass through the origin.