We get the following points from the given table.
(0,63), (12, 104), (20, 137),...,(60,106).
Consider the formula for the rate of change is
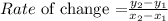
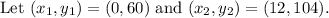
The rate of change between (0,60) and (12, 104) is

2)
The given correlation coefficient is 0.12.
Recall that correlation coefficient are used to measure the strength of the relationship between two variables.
Correlation coefficient values less than +0.8 or greater than -0.8 are not considered significant.
Given correlation coefficient is 0.12 is less than 0.8.
So this is not significant.
The answer is
There is no evidence of a relationship between age and the amount of time spent for exercise.