Question

Determine if the graphs will show parallel or perpendicular lines, or neither.6. y= -2x+12x - 4y= 48. x+ y =3X-y=510. y=2/3x-13x - 2y= 2

Answer 1

• Perpendicular lines ,have negative reciprocal slopes, meaning that if line 1 is perpendicular to line 2, then the slope of line 2 is:

`m_2=-(1)/(m_1)`

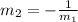
• Parallel lines ,have the same slope, meaning that is line 1 is parallel to line e, then the slope of line 2 is:

`m_2=m_1`

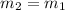
Procedure

To be able to compare each straight-line equation, we have to homogenize the form in which they are written. For example, choosing the slope-intercept form:

`y=mx+b`

where m is the slope and b is the y-intercept.

6.

In this case, the first straight-line equation is written in the slope-intercept form:

`y=-2x+1`

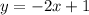
where m1 = -2.

However, we have to isolate y from the second equation in order to have it in the slope-intercept form:

`2x-4y=4`
`-4y=-2x+4`
`y=(-2x+4)/(-4)`
`y=(1)/(2)x-1`

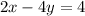
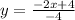
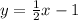
where m2 = 1/2.

If we compare these slopes:

`m_2=-(1)/(m_1)=-(1)/(-2)=(1)/(2)`

we can see that these lines are perpendicular.

8.

In this case, neither of the lines are in the slope-intercept. Thus, we have to convert them by isolating y:

• First equation

`y=-x+3`

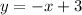
• Second equation

`y=x-5`

Again, comparing the slopes:

`m_2=-(1)/(m_1)=-(1)/(-1)=1`

therefore, these will show perpendicular lines.

10.

The first equation is in the slope-intercept form, but we have to change the second one:

`y=(3)/(2)x-1`

In this case, if we compare the slopes:

`m_2=-(1)/(m_1)=-(1)/((2)/(3))=-(3)/(2)`

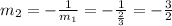
as this is not the case, these are not perpendicular lines. Also:

`m_2\\e m_1`

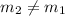
thus, these are not parallel lines. Then, these are neither perpendicular nor parallel.

Answer:

• 6. Perpendicular

,

• 8. Perpendicular

,

• 10. Neither