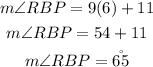Question

Let point P be in the interior of

Answer 1

Let us draw the figure to understand it

Since m

Since m

Since m

Since m

Then add (9x + 11) and (7x - 5) and equate the sum by 102

`(9x+11)+(7x-5)=102`

Add the like terms on the left side

`\begin{gathered} (9x+7x)+(11-5)=102 \\ 16x+6=102 \end{gathered}`

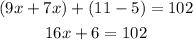
Subtract 6 from both sides

`\begin{gathered} 16x+6-6=102-6 \\ 16x=96 \end{gathered}`

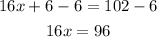
Divide both sides by 16

`\begin{gathered} (16x)/(16)=(96)/(16) \\ x=6 \end{gathered}`

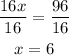
Now to find the measure of angle RBP substitute x by 6 in its measure

`\begin{gathered} m\angle RBP=9(6)+11 \\ m\angle RBP=54+11 \\ m\angle RBP=\mathring{65} \end{gathered}`