The fuction f(g(x)) is given by

The function g(f(x)) is
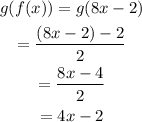
The functions f and g will be inverses of each other if the function values obtained is x in both cases. But, we got 4x+30 for f(g(x) and 4x-2 for g(f(x)), which are not equal to x. So, f and g are not inverses of each other.