Question

there are 7 women and 6 men signed up to join a swing dance class. In how many ways can the instructor choose 4 of the people to join if 1 or fewer must be men?

Answer 1

Step 1: write out the parameters given

`\begin{gathered} 7\text{women} \\ 6\text{men} \end{gathered}`

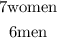
The instructor is to choose 4 people in a swing dance

Hence we have a combination

Step2: Write out the combination expression

Since one men of fewer is to be choosen then we gave

`(7C3*6C1)+(7C4+6C0)`

Srep3; Simplify the expression above

`\begin{gathered} \text{ Recall that} \\ nCr=(n!)/((n-r)!r!) \\ 7C3=(7!)/((7-3)!3!)=(7!)/(4!3!)=35 \\ 6C1=\frac{6!^{}}{(6-1)!1!}=\frac{6!}{5!1!^{}}=6 \\ \end{gathered}`

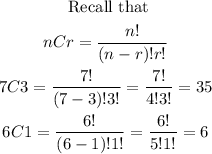
Then

`\begin{gathered} 7C4=(7!)/((7-4)!4!)=(7!)/(3!4!)=35 \\ 7C0=(7!)/((7-0)!0!)=(7!)/(7!0!)=1 \\ \text{where 0!=1} \end{gathered}`

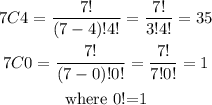
Step4: Substitute the value into the expression in step 2, we obtain

`\begin{gathered} (7C3*6C1)+(7C4+6C0) \\ (35*6)+(35*1) \\ 210+35=245 \end{gathered}`

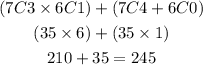
Therefore the instructor can make the choice in 245 ways