Question

Suppose that there are two types of tickets to a show: advance and same-day. Advance tickets cost $30 and same-day tickets cost $20. For one performance,there were 40 tickets sold in all, and the total amount paid for them was $950. How many tickets of each type were sold?Number of advance tickets sold: Number of same-day tickets sold:

Answer 1

Let x represent the number of advanced tickets

Let y represnet the number of same-day tickets

Sum of the tickets is 40, i.e

`x+y=40`

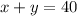
For the total amount made for ticket sold

Where

One advanced tickets, x, cost $30

One same-day tickets, x, cost $20

`\begin{gathered} 30x+20y=950 \\ \text{Divide through by 10} \\ 3x+2y=95 \end{gathered}`

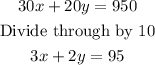
Solving simultaneously to find the number of advanced and same-day tickets sold

`\begin{gathered} x+y=40\text{ (1)} \\ 3x+2y=95\text{ (2)} \\ \text{From equation (1)} \\ x=40-y\text{ (3)} \end{gathered}`

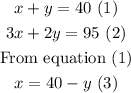
Substitute 40-y for x into equation (2)

`\begin{gathered} 3(40-y)+2y=95_{} \\ 120-3y+2y=95 \\ 120-y=95 \\ \text{Collect like terms} \\ y=120-95 \\ y=25 \end{gathered}`

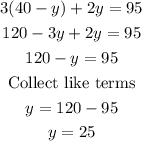
Substitute 25 for y into equation (3)

`\begin{gathered} x=40-y \\ x=40-25 \\ x=15 \end{gathered}`

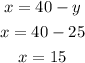
Hence, the number of advanced tcikets, x, sold is 15

And the number of same-day tickets, y, sold is 25