Question

7.2.2 Practice 3 A map of a rectangular park has a length of 4 inches and a width of 6 inches. It uses a scale of 1 inch for every 30 miles. 1. What is the actual area of the park in square miles?

Answer 1

To answer this question, we can proceed as follows:

1. We have that the scale is 1 inch represents 30 miles.

Then, with this factor we can find the actual area of the park in square miles, as follows:

`4in\cdot\frac{30\text{miles}}{1\text{inch}}=(4in\cdot30miles)/(1inch)=120\text{miles}`

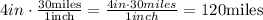
We use the scale factor to find the actual value for the length of 4 inches. We can use the same for the width of the map:

`6in\cdot(30miles)/(1inch)=(6in\cdot30miles)/(1inch)=180\text{miles}`

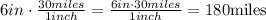
Now, the actual area of the park in square miles is:

`A_{\text{park}}=120\text{miles}\cdot180\text{miles}=21600\text{miles}^2`

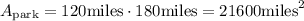
Therefore, the actual area of the park is 21,600 square miles.