SOLUTION
The image is given below
From the image above, the angle is a right angle
Hence
The sum of the measure of angle 1 and measure of angle 2 is 90 degrees
i.e

Substitute the expression for angle 1 and angle 2, we obtain
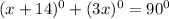
Simplifying the equation we have
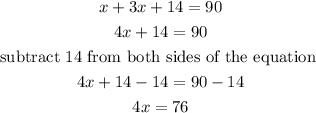
Hence, the equation to find x is
4x=76
To find the measure of each angle we need the know the value of x

Hence the value of x is 19
Hence the measure of angle 1 will be
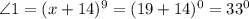
The measure of angle 1 is 33°
Similarly, we substitute x for the measure of angle 2
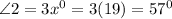
The measure of angle 2 is 57°