1 Answer

Keshan Nageswaran · Answer 1 · 2023-11-17T16:38:59+0000

From the attached picture we can see

The right triangle NPR

NP and PR are its legs

NR is the hypotenuse

x and y are the measures of the 2 acute angles

To find x, we can use the sine ratio

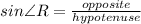
$sin\angle R=(opposite)/(hypotenuse)$

The opposite side is NP = 60

The hypotenuse is NR = 87

Substitute them in the ratio

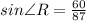
$sin\angle R=(60)/(87)$

Use the inverse of the sine

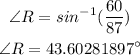
$\begin{gathered} \angle R=sin^(-1)((60)/(87)) \\ \angle R=43.60281897^(\circ) \end{gathered}$

Round it to the nearest whole number, then

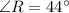
$\angle R=44^(\circ)$

Since x is the measure of angle R, then

x = 44

Since the sum of the measures of the angle of a triangle is 180 degrees, then

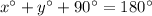
$x^(\circ)+y^(\circ)+90^(\circ)=180^(\circ)$

Substitute x by 44

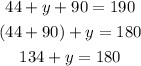
$\begin{gathered} 44+y+90=190 \\ (44+90)+y=180 \\ 134+y=180 \end{gathered}$

Subtract 134 from both sides

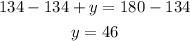
$\begin{gathered} 134-134+y=180-134 \\ y=46 \end{gathered}$

The answers are:

x = 44

y = 46

Please log in or register to add a comment.