The alternatives indicates that the question is aboud even and odd function.
An even function is one the gives:
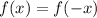
While an odd function is one tha gives:
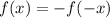
The fisrt function is:

Since
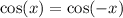
Then
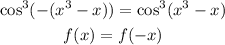
So, f is even.
We can do it similarly for g(x)
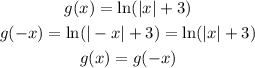
For s(x), we have:
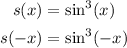
Since:
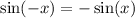
Then:
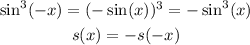
So far we have f(x) even, g(x) even and s(x) odd. This is exactly what is said in alternative A:
A. f and g are even, s is odd.
so that is the right answer.