Let's put more details in the given graph:
For us to be able to determine the equation of the given graph, we will be applying the following formula:
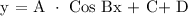
Where,
A = Amplitude
B = 2π/Period
C = Phase Shift
D = Vertical Shift
Let's determine their values.
A = Amplitude
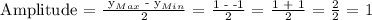
Therefore, the Amplitude is 1.
B = 2π/Period
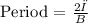

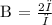
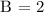
Therefore, B = 2
C = Phase Shift
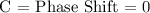
D = Vertical Shift
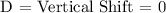
In Summary, we have A = 1, B = 2, C = 0 and D = 0.
Let's now plug it to the formula to get the equation of the graph.
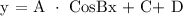
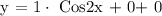
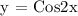
Therefore, the equation of the graph is y = Cos(2x).
The answer is CHOICE B : y = cos(2x)