Assuming the distribution of the test scores is approximately normal, we calculate the percentages as cumulative probabilities of the bell curve.
To do that, we use Excel. You could use any other digital means or technology.
The z-score is defined as:
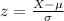
Where X is the score whose probability we want to calculate, μ is the mean, and σ is the standard deviation.
1. Calculate the percentage of students who scored less than 61 on the test.
The z-score is:
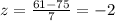
Now determine the probability p(z < -2) with Excel:
p(z < -2) = 0.02275
Multiplying by 100:
Required percentage = 2.275%
2. Calculate the percentage of students who scored between 61 and 89 on the test.
We calculate P(X < 61), P(X < 89) and subtract the results.
We have already calculated P(X < 61). Now calculate P(X < 89).
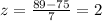
Now determine the probability p(z < 2) with Excel:
p(z < 2) = 0.97725
Multiplying by 100:
p(z < 2) = 97.725%
p(z < 2) - p(z < -2) = 97.725% - 2.275% = 95.450%
3) Calculate the percentage of students who scored between 68 and 75 on the test.
P(68 < X < 75) = P(X < 75) - P(X < 68)
Calculating the probabilities with Excel:
P(68 < X < 75) = 0.5 - 0.34134