Answer
• a) Range: (-∞, –1)
• b) Horizontal asymptote when x ≤ 2: y = –3. Vertical asymptote when x > 2: x= 2. Horizontal asymptote when x > 2: y = –1.
,
• c) When x decreases, it approaches –3, and when x increases, it approaches –1.
Step-by-step explanation
• Part A: Graph the piecewise function f (x) and determine the range.
Using a graphing tool we can get the following graph:
As the range is all the y-values included in the function, we can see that in this case, the range is:
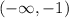
• Part B: Determine the asymptotes of f (x). Show all necessary calculations.
We have to get the asymptotes from the part where x ≤ 2 and x > 2.
In x ≤ 2 we do not have a vertical asymptote as it is not a rational function, but we do have a horizontal asymptote, which is y = k when we have the function:
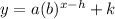
Thus, in our case y = –3.
In x > 2, we do have a vertical and horizontal asymptote. We can get the vertical asymptote by setting the denominator of the function to 0:

If we solve the expression by factoring we get two solutions:


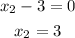
Based on our function we can see that the vertical asymptote is x = 2 when x > 2. Then, the horizontal asymptote can be calculated with the limit:
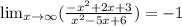
Thus, our horizontal asymptote is y = –1 when x > 2.
• Part C: Describe the end behavior of f (x).
The end behavior of a function is how the function acts when x increases or decreases. Based on our graph we can see that when x decreases, it approaches –3, and when x increases, it approaches –1.