ANSWER
x = 3 + 2i or x = 3 - 2i
Explanation:
Given the polynomial equation below
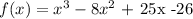
From the question provided, you can see that x= 2 is one of the zero of the above polynomial.
Therefore, we can find the other zeros by first finding the equation by x - 2 using long division
From the calculation above, the quotient is given as
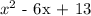
The next step is to solve the quadratic equation using the general formula
Recall that, the standard quadratic equation is given below as
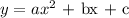
Hence,
a = 1
b = -6
c = 13
![\begin{gathered} \text{General quadratic formula is} \\ x\text{ }\frac{-b\text{ }\pm\sqrt[]{b^2\text{ - 4ac}}}{2a} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/saojrromsiof7zaexmfq5u3vk26fcn7cy7.png)
Substitute the values of a, b, and c into the formula
![\begin{gathered} x\text{ = }\frac{-(-6)\pm\sqrt[]{(-6)^2\text{ - 4 }\cdot\text{ 1 }\cdot\text{ 13}}^{}}{2\cdot\text{ 1}} \\ x\text{ = }\frac{6\text{ }\pm\sqrt[]{36\text{ - 52}}}{2} \\ x\text{ = }\frac{6\pm\sqrt[]{-16}}{2} \\ \text{ }\sqrt[]{-16}\text{ = }\sqrt[]{-1}\cdot\text{ }\sqrt[]{16} \\ \text{where }\sqrt[]{-1}\text{ = i and }\sqrt[]{16}\text{ = 4} \\ \sqrt[]{-16}\text{ = 4i} \\ \text{Therefore, } \\ \text{x = }\frac{6\text{ + 4i}}{2}\text{ or }\frac{6\text{ - 4i}}{2} \\ \text{x = }3\text{ + 2i or x = 3 - 2i} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6qvrj254q1w9myfw05hfb5l1c1fgr496yq.png)
Therefore, the other zero values are, 3 + 2i and 3 - 2i