Answer:
362
Step-by-step explanation:
Given the cost function, C(x), and total revenue, R(x), as;
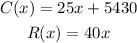
Recall that the profit function, P(x), is given as;

Note that a break-even point is a point where the revenue starts overtaking the cost. At the break-even point, P(x) = 0, so we'll have;
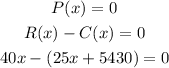
Let's clear the parentheses and solve for x;
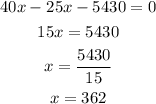
We can see from the above that the number of widgets the manufacturer has to sell to break even is 362