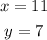Use the substitution method to solve the system of equations:
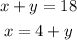
Since x is already isolated on the second equation, replace x with the expression for x in the first equation:
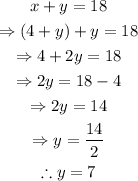
Substitute y=7 into the expression for x:
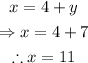
Therefore, the solution for this system of equations, is: