Step 1
The total probability of event happening + event not happening = 1
Assuming the order of rain does not matter there are 6 possibilities;
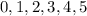
The probability being asked for is if the number of days is at least 1. That is;
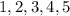
Therefore, we can find the probability of no rain happening. That is 0. Then subtract it from 100%.
The probability of no rain happening for 1 day is
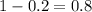
So the probability of rain not happening everyday is;
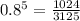
Therefore, the probability of rain happening at least once is;
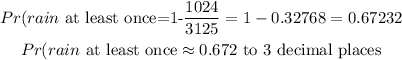
Answer;
