Consider that the point-slope form suggests that the equation of a straight line having slope 'm' and passing through a point, is given by,
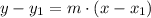
Given that the slope of the line is 0,
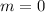
Also, the line passes through the point,
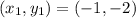
Substitute the values,
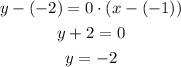
Thus, the equation of the line having slope 0 and passing through (-1,-2) is obtained as,
