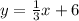Question

Whats the parallel equation of y=1/3x-2 goes through point (0,6)

Answer 1

You know that two lines are parallel if they have the same slope, so the new line will also have slope

`m=(1)/(3)`

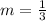
Because the equation of the given line is written in the form

`\begin{gathered} y=mx+b \\ \text{Where} \\ m\colon\text{slope of the line} \\ b\colon\text{ y-intercept} \end{gathered}`

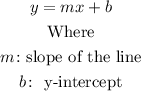
Then, you can use point slope equation, which is

`\begin{gathered} y-y_1=m(x_{}-x_1) \\ \text{Where} \\ (x_1,y_1)\colon\text{ point through which the line passes.} \\ m\colon\text{slope of the line} \end{gathered}`

So,

`\begin{gathered} (x_1,y_1)=(0,6) \\ \text{ And you have} \\ y-y_1=m(x_{}-x_1) \\ y-6=(1)/(3)(x-0) \\ y-6=(1)/(3)x-0 \\ y-6=(1)/(3)x \\ \text{ Add 6 to both sides of the equation} \\ y-6+6=(1)/(3)x+6 \\ y=(1)/(3)x+6 \end{gathered}`

Therefore, the equation of the line that is parallel to y=1/3x-2 and goes through point (0,6)​ is

`y=(1)/(3)x+6`