Question

Find a parallel equation to the line g(x) = 3x - 4 and a perpendicular equation that passes through the point (0, -4)

Answer 1

To answer this question, we can proceed as follows:

1. Parallel equation to g(x) = 3x - 4 that passes through the point (0, -4).

Two lines are parallel if they have the same slope. In this case, the slope is represented by m = 3. Then, using the Point-Slope Form of the line equation, we have:

`y-y_1=m(x-x_(1))\Rightarrow y-(-4)=3(x-0)\Rightarrow y+4=3x\Rightarrow y=3x-4`

As we can see, in this case, the original equation passes through this point too. Therefore, we can write a parallel line to the original if we preserve the slope. Therefore, we can say that:

`y=3x,y=3x+1,y=3x+5`

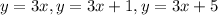
We can select one of them to answer this part of the question.

They are all parallel to the original equation g(x) = 3x -4.

2. Perpendicular equation to g(x) = 3x - 4 that passes through the point (0, -4).

In this case, one line is perpendicular to another line if we take the reciprocal and the inverse of the original line, that is if we have that m = 3, then, for a perpendicular line, the slope will be:

`m_1=-(1)/(3),3\cdot(-(1)/(3))=-1`

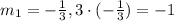
The product of both slopes is -1.

Therefore, we can also apply the Point-Slope Form of the line equation in this case, taking into account the point (0, -4). Then, we have:

`y-y_1=m(x-x_1)\Rightarrow y-(-4)=-(1)/(3)(x-0)\Rightarrow y+4=-(1)/(3)x_{}`

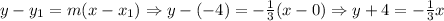
Thus, the perpendicular line is:

`y=-(1)/(3)x-4`

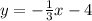
We can see that the red line is represented by y = 3x - 4 (red line), the blue line by y = 3x, and the green line by y = -(1/3)x - 4 (see that the line passes through the point (0, -4)).