we are given the following expression:
![a\sqrt[]{x+b}+c=d](https://img.qammunity.org/2023/formulas/mathematics/college/xgpm4xm0jkr7h5lt0ototg217olgbzy1lp.png)
We are asked to find constants a, b, c, and d such that we get an extraneous solution and a non-extraneous solution.
Let's remember that an extraneous solution arises when solving a problem we reduce it to a simpler problem and get a solution but when replacing that solution in reality it's not a solution to the problem because it is undetermined or outside the domain of the original problem.
Part 1. Let's choose the following values:

We get the equation:
![2\sqrt[]{x-5}+8=4](https://img.qammunity.org/2023/formulas/mathematics/college/tvvfecmwprrozj2u5rlvyszuoec2g9jmut.png)
Now let's take the following values for the constants:

We get the equation:
![2\sqrt[]{x-5}+4=8](https://img.qammunity.org/2023/formulas/mathematics/college/rdyomco7i13d419r1qgyt0ip5x0wlmxx6f.png)
Part 2. To get the extraneous solution we will isolate the radical first from the expression. To do that we will subtract "8" from both sides:
![2\sqrt[]{x-5}=4-8](https://img.qammunity.org/2023/formulas/mathematics/college/pw91omuxv95t2234rocniwwn9nk88vj50o.png)
Now we'll divide by "2":
![\sqrt[]{x-5}=(4-8)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/4f5fkiv4z6rzssi00vdhr1bs2yq7shcgx4.png)
Let's choose the following values:

Now let's solve for "x":
![\sqrt[]{x-5}=-(4)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/1on58fa32hxiqx34ywxp5virx5jut5yjcq.png)
![\sqrt[]{x-5}=-2](https://img.qammunity.org/2023/formulas/mathematics/college/jly88faykyrzq4xm4d3c4k81o0qobz4evr.png)
Elevating both sides to the second power:
![(\sqrt[]{x-5})^2=(-2)^2](https://img.qammunity.org/2023/formulas/mathematics/college/fa8uonop7aygdcn06mnr3wdddtzhqgqxtg.png)
Solving:
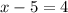
Adding 5 on both sides:
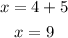
Now that we get a solution we need to check it by replacing the value we found for "x" in the initial equation:
![\sqrt[]{x-5}=-2](https://img.qammunity.org/2023/formulas/mathematics/college/jly88faykyrzq4xm4d3c4k81o0qobz4evr.png)
Replacing the value of "x":
![\sqrt[]{9-5}=-2](https://img.qammunity.org/2023/formulas/mathematics/college/6m7h7ws8941ronea369uld41nrhjkdkzsd.png)
Solving the operation inside the radical:
![\sqrt[]{4}=-2](https://img.qammunity.org/2023/formulas/mathematics/college/ttvhri06n3kcnpqyd0hkok1zhrfmnoymkb.png)
Solving the radical:
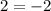
Now we use the second equation:
![2\sqrt[]{x-5}+4=8](https://img.qammunity.org/2023/formulas/mathematics/college/rdyomco7i13d419r1qgyt0ip5x0wlmxx6f.png)
Isolating the radical we get
![\sqrt[]{x-5}=(8-4)/(2)](https://img.qammunity.org/2023/formulas/mathematics/college/dm6ztowqbl2uinxzgotzwv26f0a521ldzk.png)
Solving the operations:
![\begin{gathered} \sqrt[]{x-5}=(4)/(2) \\ \sqrt[]{x-5}=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1qh8vd2j60a3motpbu7tx8worbnsw7mn9h.png)
Squaring both sides:
![(\sqrt[]{x-5})^2=(2)^2](https://img.qammunity.org/2023/formulas/mathematics/college/j8jb0m8svincfe46rgsxfedcd0bovg2cwb.png)
Solving the square:
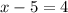
adding 5 on both sides:
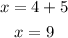
Now, replacing the value of "x" in the original equation:
![\sqrt[]{9-5}=2](https://img.qammunity.org/2023/formulas/mathematics/college/vv2itpnditt0qng8fc38oqa710fxc810ta.png)
Solving the operation inside the radical:
![\sqrt[]{4}=2](https://img.qammunity.org/2023/formulas/mathematics/college/jp883cq2swgjs5b0eu3u3mzbbms7owh6dt.png)
Solving the radical.

Therefore, x = 9 is a solution to this equation.
Part 3. Since the value we found for "x" in the first equation does not give a solution, this means that x = 9 is an extraneous solution for the first given values of the constants.