Question

`{2}^(3) * {4}^(n) = {2}^(11)`2^3 x 4^n = 2^11Find the value of the variable.

Answer 1

n = 4

Step-by-step explanation:

To find the value of n, we will use the following properties:

`\begin{gathered} (2^a)/(2^b)=2^(a-b) \\ 4^n=2^(2n) \end{gathered}`

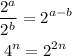
Now, we have the expression:

`2^3\cdot4^n=2^(11)`

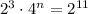
Divide both sides by 2³, so:

`\begin{gathered} (2^3\cdot4^n)/(2^3)=(2^(11))/(2^3) \\ 4^n=2^(11-3) \\ 4^n=2^8 \end{gathered}`

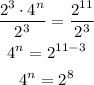
Then, we can replace 4^n by 2^(2n), so:

`2^(2n)=2^8`

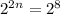
Since the base on both sides is equal to 2, we can equal the exponents, so:

`2n=8`

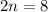
Finally, divide both sides by 2, so:

`\begin{gathered} (2n)/(2)=(8)/(2) \\ n=4 \end{gathered}`

So, the value of n is 4.